Numerical example
Consider a Stable Pool containing USDC and USDT, where USDT has slightly de-pegged (say, to 0.98).
p₁ = $1.00 (USDC), p₂ = $0.98 (USDT)
A = 100, D = 1000 (invariant)
Step 1: Calculate the parameters (amplification coefficient, and "helper" constants derived from the Amplification parameter)
a = A × n^(2n) = 100 × 2^4 = 1600
b = a - n^n = 1600 - 2^2 = 1596
c = b/a = 1596/1600 = 0.9975
Step 2: Calculate the r values (scaled prices)
r₁ = p₁/a = 1.00/1600 = 0.000625
r₂ = p₂/a = 0.98/1600 = 0.0006125
Step 3: Find the root, using Newton's method:
Choose the starting point: k₀ = (1 + 1/(1+b)) × ρ
k₀ = (1 + 1/(1+1596)) × 1633 = (1 + 1/1597) × 1633 ≈ 1634.02
Newton's method:
kₙ₊₁ = kₙ − G(kₙ) / G′(kₙ); where
G(k) = T(k)³ × P(k) - α
G'(k) = T²(k) × P(k) × [(3T'(k) × P(k) + T(k) × P'(k))/P(k)]
And: T'(k) = -r₁/(kr₁-1)² - r₂/(kr₂-1)²
P'(k) = P(k) × [r₁/(kr₁-1) + r₂/(kr₂-1)]
First iteration (k₀ = 1634.02)
Calculate T(1634.02):
T = 1/(1634.02×0.000625-1) + 1/(1634.02×0.0006125-1) - 1
T = 1/(1.0213-1) + 1/(1.0008-1) - 1
T = 1/0.0213 + 1/0.0008 - 1 = 46.95 + 1250 - 1 ≈ 1295.95
Calculate P(1634.02):
P = (1634.02×0.000625-1) × (1634.02×0.0006125-1)
P = 0.0213 × 0.0008 ≈ 0.000017
Calculate G(1634.02): the "error"
G = (1295.95)³ × 0.000017 - 1588.03
G = 2.17×10⁹ × 0.000017 - 1588.03 ≈ 36,890 - 1588 ≈ 35,302
Calculate derivatives and find k₁:
T' = -0.000625/(0.0213)² - 0.0006125/(0.0008)² ≈ -1380 - 956 ≈ -2336
G' ≈ ... (complex calculation) ≈ 50.8
k₁ = 1634.02 - 35,302/50.8 ≈ 1634.02 - 694.9 ≈ 939.1
Continue iterations:
| Step | k̃ₙ | G(k̃ₙ) | k̃ₙ₊₁ |
|---|---|---|---|
| 0 | 1634.02 | 35,302 | 939.1 |
| 1 | 939.1. | -285.4 | 1425.7 |
| 2 | 1425.7 | 892.1 | 1580.3 |
| 3 | 1580.3 | 124.7 | 1635.8 |
| 4 | 1635.8 | 8.2 | 1640.1 |
| 5 | 1640.1 | 0.1 | 1641.0 |
| 6 | 1641.0 | ~0 | 1641.0 |
Graphical representation of the T curve:
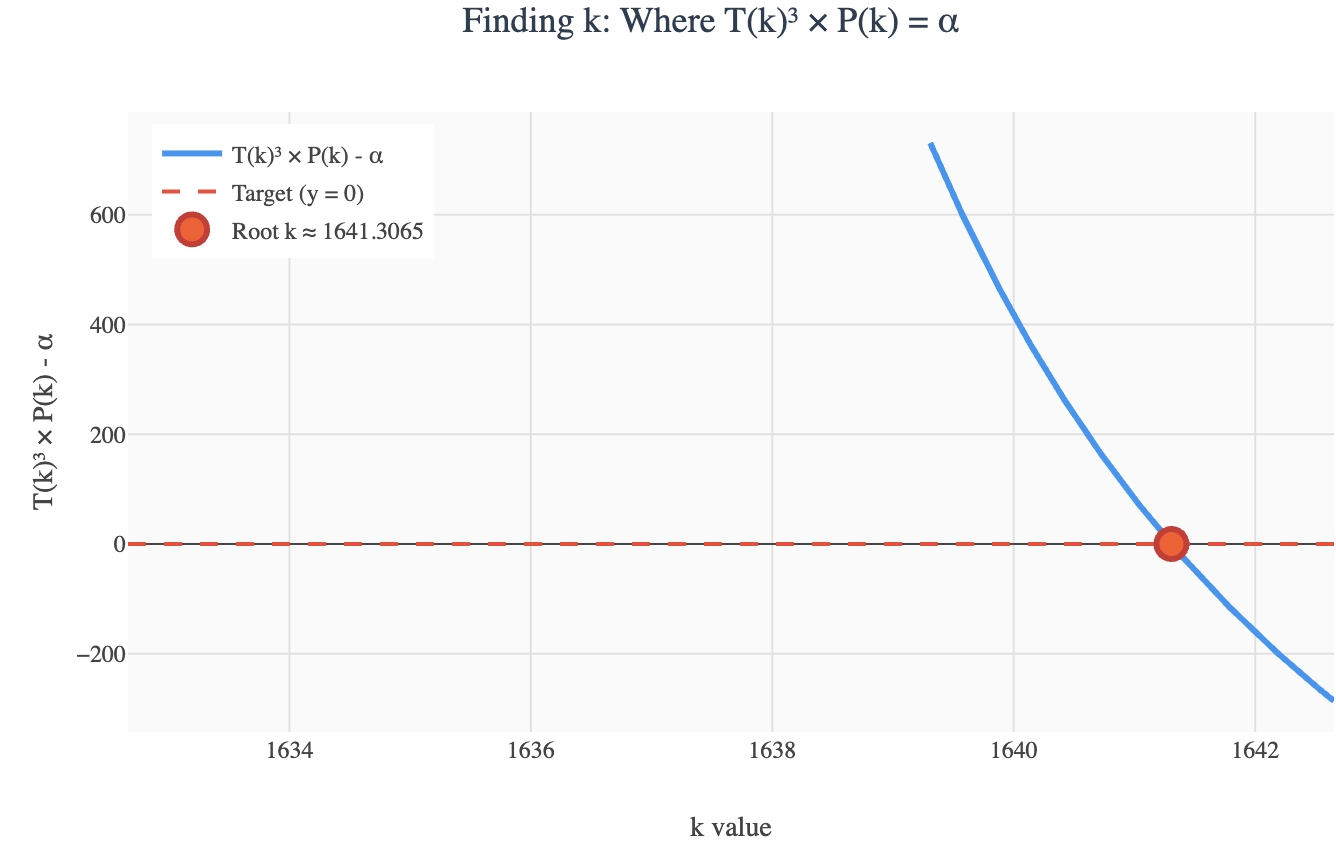
Step 4: Calculate T (using our found k̃ = 1641)
Recall that T = 1/(k̃r₁ - 1) + 1/(k̃r₂ - 1) - 1
T = 1/(1641 × 0.000625 - 1) + 1/(1641 × 0.0006125 - 1) - 1
T = 1/(1.025625 - 1) + 1/(1.0051125 - 1) - 1
T = 1/0.025625 + 1/0.0051125 - 1
T = 39.02 + 195.60 - 1 = 233.62
Step 5: Calculate effective balances
Recall that x₁ = (cD)/(k̃r₁ - 1) × T⁻¹
x₁ = (0.9975 × 1000)/(1641 × 0.000625 - 1) × (1/233.62)
x₁ = 997.5/0.025625 × (1/233.62) = 166.69
x₂ = (cD)/(k̃r₂ - 1) × T⁻¹
x₂ = (0.9975 × 1000)/(1641 × 0.0006125 - 1) × (1/233.62)
x₂ = 997.5/0.0051125 × (1/233.62) = 833.31
Step 6: Calculate total pool value
Recall that Pool Value = p₁ × x₁ + p₂ × x₂
Pool Value = $1.00 × 166.69 + $0.98 × 833.31
Pool Value = $166.69 + $816.64 = $983.33
Step 7: Calculate BPT price
Recall that BPT Price = Pool Value / Total BPT Supply
(If total BPT supply = 1000 tokens, since D = 1000, and starting prices were nominal at $1)
BPT Price = $983.33 / 1000 = $0.983 per BPT