Impermanent Loss
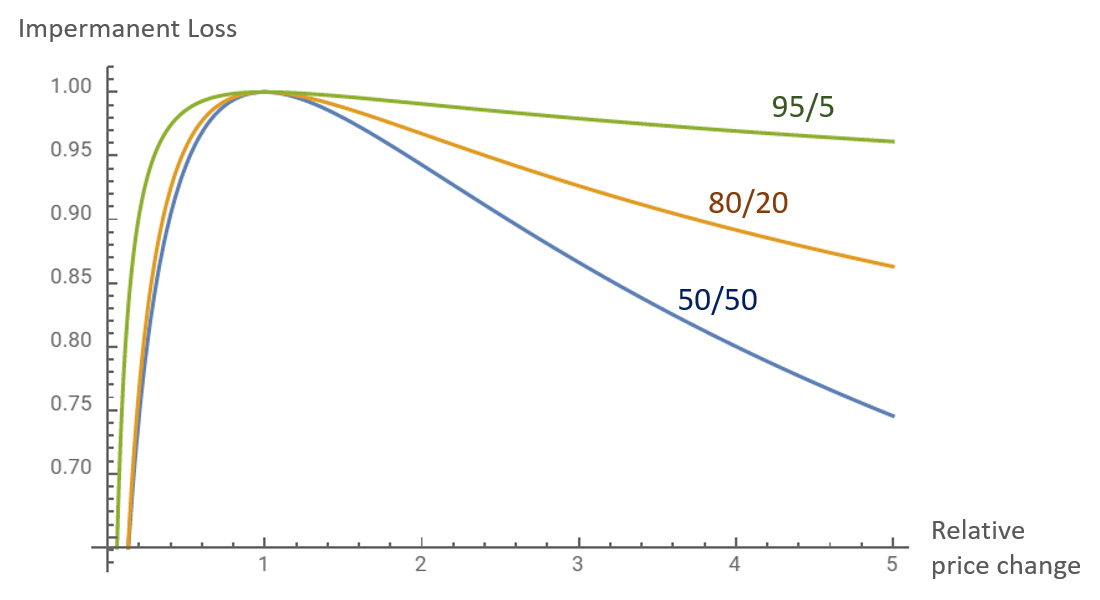
Impermanent Loss, sometimes referred to as divergent loss, is simply the opportunity cost of adding liquidity into an AMM pool vs. holding the individual tokens.
Impermanent loss occurs when the prices of two assets diverge in price after initial liquidity provision. For example, if all assets in a pool increase by 20%, there is no impermanent loss. However, if only one asset increases in value by 20%, uncorrelated with the other tokens, there will be some impermanent loss. It is "impermanent" because it can be reversed; e.g., if the asset returned to its initial value, or the other tokens also increased 20%. For a basic example of impermanent loss followed by a reversal, see the next page.
50/50 Pools
We will start with a simple 50/50 pool featuring COMP/WETH. We want to deposit $5,000 worth of each token, for a total value of $10,000. At initial investment time, WETH is priced at $2,000, and COMP is $250, so we deposit 2.5 WETH and 20 COMP.
Some time later, we find that COMP has doubled to $500, while WETH has increased 15%, to $2,300. Although the value of the position has gone up along with the tokens, any uncorrelated deviation from the initial prices will result in some level of impermanent loss: we are missing out on some portion of the theoretical gains.
Here we calculate the invariant from the value function:
Our gains will be determined by the invariant ratio, this value can be used for our token balances as well.
Here we can consider the USD values to be the same in the numerator and denominator therefore not needed to determine the ratio between the two.
For the new token balances we consider the invariant ratio compared to the price action of the individual asset. This proportion will yield the new balance of each token in relation to the initial join amount.
Please note these calculations can take place over any time frame. These occurred in roughly 12 days between June 25th and July 7th, 2021. This same price action could just as well take place over the course of 1 year. With 4% or more in swap fees or liquidity mining incentives, the LP position would become the more attractive option.
These calculations are depicted by the following tables.
Initial Liquidity Position Amount: $10,000.00
HODL Total: $15,750.00
LP Total $15,165.75; with 4% Annual yield $15,772.38
In our prior example, COMP and WETH went through uncorrelated price changes, and we observed the potential loss of value through impermanent loss. Now, if the prices continue to change, we will look at an example where WETH goes up to $3,000.00, while COMP decreases to $375.00. Perhaps surprisingly, this leads to a 50% gain in both assets relative to our original Liquidity Position.
Therefore, because the invariant ratio matches the price ratio, there will be no impermanent loss.
This calculation will be performed from the impermanent loss state to the current state, in order to prove that the “loss” is indeed reversible under the proper conditions.
Initially:
After Price Change:
New Token Balances can be calculated as follows:
These balances match our initial liquidity position, meaning overall we lost nothing to impermanent loss. The price action is still in our favor by 50% for both assets as we hold the same initial number of each. Also, we would have likely collected swap fees from traders, making our gains slightly larger.
This shows that even large impermanent losses can always be reversed through subsequent price action. This can occur countless times as the asset prices in a pool fluctuate. It is important to understand the assets you are holding and how comfortable you are with volatility. In theory, great volatility will be coupled with large swap volumes, making the swap fees and gains for liquidity providers increase. Weighing the risk of impermanent loss against the accumulation of swap fees or “volatility farming” is the game a liquidity provider is playing over the long term.
80/20 Pools
Here we will examine how disproportionate pool weights affect the calculation of impermanent loss, using the same scenario described above, but for an 80/20 vs. a 50/50 pool.
COMP WETH 80/20
To illustrate the benefits of uneven pool weights, we calculate impermanent loss under conditions favoring COMP. We will hold 1 WETH @ $2000.00 and 32 COMP @ $250.00. ($8,000 in COMP and $2,000 in WETH: same $10,000 total as before).
Our gains will then be determined by the invariant ratio. This can be used for our token balances as well.
Here we can consider the USD values to be the same in the numerator and denominator, so we don't need to determine their ratio.
While impermanent loss still occurs in this scenario, the losses are nearly cut in half compared to the 50/50 pool (reduced by a factor of 0.5825, to be precise). When dealing with very large liquidity positions, these small amounts can make a large difference in value. Ultimately, this weighting strategy can protect liquidity providers from impermanent loss: or actually increase their exposure, depending on their token choices. Of course, if prices return to their initial values, or move proportionally, at a certain point the “losses” will revert to zero regardless of the weights.
Multi-token Pools
Balancer's multi-token pools are one of our unique features. Below is an example of how impermanent loss on one of these pools can occur, including details on volatility and stable coins.
Advanced Example – Multi-token Pool
Below we show an example of a multi-token pool, and how impermanent loss can occur and then be reversed. We will look at a Polygon pool: 25% USDC, 25% WMATIC, 25% BAL, 25% WETH. Initially we will assume we joined with $10,000 in USD, distributed evenly over all the assets.
Initial Conditions:
We will assume USDC stays at a constant value, BAL increases by 15% to $28.75, WMATIC decreases by 4% to $1.20, and WETH increases 50% to $3,750.00.
New Token Balances can be calculated as follows:
Since the pool contains a stable coin (USDC), impermanent loss is nearly inevitable unless all tokens return to their initial value at the time of liquidity provision. Therefore, Liquidity Providers for the pool above or any pool combining stable and non-stable assets should mostly be concerned with volatility and earning a return from swap fees or liquidity mining incentives. They are essentially positioning themselves with the expectations of this type of price pattern: 
One may provide liquidity to a pool in which USDC and an asset (X) at 14.01 are present in mid-July. Then by the time the chart comes to an end the price is still 14.01 after going through stages of upward and downward price changes. This will yield an amount of swap fees to be collected as profit as well as 0% impermanent loss.
At any point when all prices revert to their initial values, arbitragers will bring the tokens back to their initial balances. With a stable token present, this means no gains can be made without impermanent loss or swap fees.
