# Readjusting Concentrated Liquidity AMM Pool Math

# Intro

The Readjusting Concentrated Liquidity AMM (reCLAMM) is a pool based on a "constant product," essentially equivalent to standard weighted math (with a clever redefinition of the token balances). The idea is to concentrate liquidity by adding price bounds to the constant product curve using virtual balances: , where and are the real balances of the token, and and are the virtual balances of the token.

Currently, in fungible concentrated liquidity pools with fixed price intervals, LPs may need to actively migrate liquidity between CL pools to avoid losing fee revenue to pools that have gone out of range. The Readjusting CL AMM is a pool that automatically readjusts the price interval, so that a retail LP can confidently deposit assets and rely on the pool to manage them efficiently and profitably.

# Concepts

# Virtual Balances

Virtual Balances can be understood as offsets to the real token balances, so that the balances of the pool are never lower than the virtual balance. (balance = real balance + virtual balance)

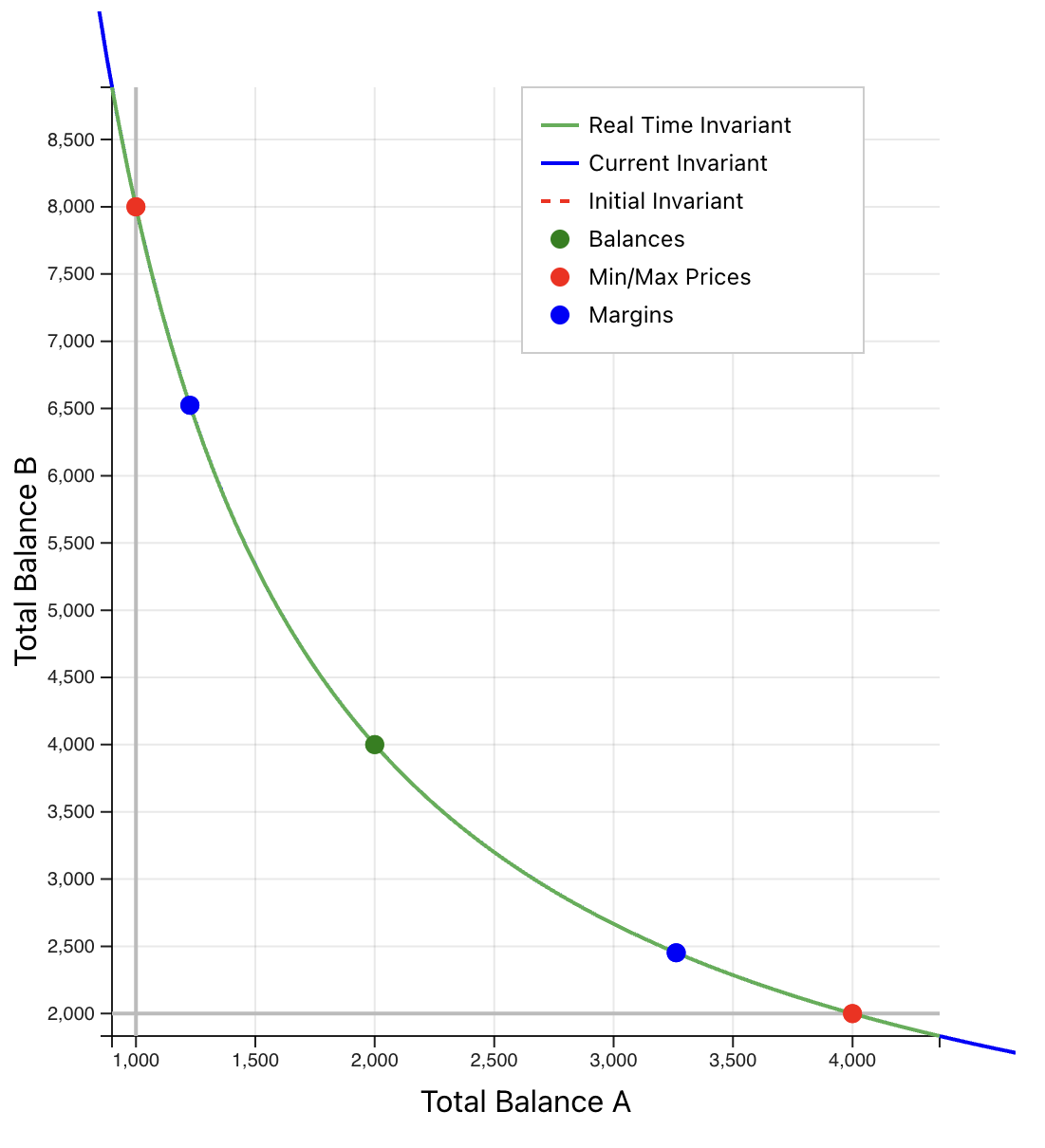
Therefore, even if the real balance of a token goes to zero, the virtual balance will keep the token balance (and therefore price) above zero. In practice, it restricts the token price between two bounds, defined by the virtual balances of each token. The image below illustrates a constant product price curve with hard price limits, "soft" margins (described later - basically the threshold where the pool will begin self-adjusting), and the "target" price, usually close to the middle of the range.

# Initial Virtual Balances

During pool creation, the pool creator will define the minimum price () and the maximum price (). Given these three parameters, we can calculate the initial virtual balances.

The invariant of a reCLAMM Pool is calculated as follows:

Where and are the real balances, and are the virtual balances, and is the invariant. The current price of the pool is given by:

Note that we have (arbitrarily) defined it as B/A (i.e., prices represent the value of token A denominated in token B. In other words, how many B tokens equal the value of one A token.)

Given the price formula, we know that the minimum price happens when the denominator takes on its maximum value: . In this state, . (At the edges, one of the balances will be maximum, and the other balance will be 0). Before the initialization of the pool the "maximum" balance is not known - so, to calculate the initial balances of the pool, we set the maximum balance of token A to an arbitrary value, and then we can scale accordingly when the initialization amounts are known:

Since the invariant is constant, we can deduce that the invariant formulas in these two edge points are, respectively:

One last concept important to calculate the initial virtual balances is the price ratio, defined in the next section. Since , substituting the max and min price formulas, we have:

Using the two invariant formulas for the edges, we have

Now we have a way to calculate the invariant based on the virtual balances. Since ,

Now we need a way to use these prices to calculate and . Since the virtual balances are proportional to the real balances, we will randomly choose a , which will allow us to calculate and . When the pool is initialized we can find and by multiplying the and by the rate , where is calculated based on the initialization balances.

So, using the invariant , we have that

cancels out, so we can isolate :

Using the formula, we have:

# Initial Real Balances

Now we need to find the balances and corresponding to the desired target price (), which was also given by the user when the pool was created. These values will be used to inform the initializer of the pool of the correct token proportion required to initialize the pool at the given target price.

To calculate it, let's use , and .

Using the invariant formula in , we have that .

Since , , which leads to

Then, isolating in the formula, we have

# Balance Ratio

As noted above, the Balance Ratio is the proportion of token B in relation to token A that must be used to initialize the pool, so that the target price is respected.

# Initialization

Finally, when initializing, we need to scale and to the initial balances of the pool. The scale is (which is the same rate as ). So

# Price Ratio ()

The Price Ratio is the ratio between the high and low price bounds of the range. The current price of token A is defined as .

The highest price of A () is reached when the real balance of A is 0. So, the price is defined as:

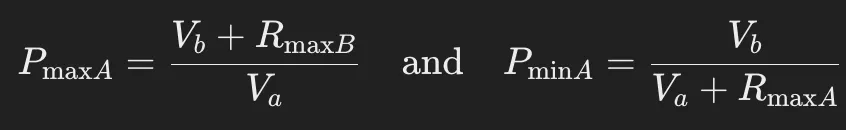
The Price Ratio is calculated as .

For example, let's say the pool has virtual balances of 1000 of each token. Also, let's assume that when the real balance of token A is 0, token B is 1000 (), and vice versa.

In the example, and , so .

# Price Ratio Update

The Price Ratio can be updated by a pool manager. This update is gradual, analogous to updating the amplification factor of a Stable Pool. The pool manager defines a start and end time and a target , and then is calculated as an interpolation between the initial and final values, and .

# Pool Centeredness

As noted above, the main idea of this pool is to manage the price interval such that the market price stays within it as much as possible. The pool won't use an external oracle, so we need a mechanism to determine whether the market price is within the current price interval: Pool Centeredness.

Pool Centeredness is a number (a percentage) that describes how far the pool balances are from the center of the current interval. The number goes from 0 to 1, where 0 means that the balances are at the edge and 1 means that the balances are exactly in the middle of the current price range, which is the case when the pool is initialized. The number is calculated as follows:

1. First, if or are 0, we know that pool centeredness is 0.
2. If not, we calculate and compare with . Since the virtual balances were calculated based on the real balances, these rates are the same near the center of the interval.

   1. If ,

   2. Otherwise,

# Pool Centeredness Margin

We could wait for the centeredness to be zero before moving the price interval, but that means we would wait for one of the real balances to be zero, which in practice means no exposure to one of the assets of the pool, and lost trade opportunities. The balance doesn't have to literally go to zero for the pool to get "stuck"; there could also be a dust balance worth less than the gas required to arb it. To avoid this situation, we introduce the concept of Centeredness Margin (see the image above used to illustrate the concept of virtual balances).

Margin is a number (also a percentage) from 0 to 1, very similar to pool centeredness, and helps calculate whether the pool is IN RANGE (Pool Centeredness > Margin) or OUT OF RANGE (Pool Centeredness ≤ Margin). If the pool is OUT OF RANGE , the price interval will be recalculated (which, in practice, means that we will recalculate the virtual balances).

# Daily Price Shift Exponent

The Daily Price Shift Exponent is a percentage that defines the speed at which the virtual balances will change per day. A value of 100% (i.e, FP 1) means that the min and max prices will double (or halve) every day, until the pool price is within the range defined by the margin. We use the following formula to calculate the current virtual balance of a token:

where is a time constant, defined as . If we want in the following day, DailyPriceShiftExponent = 100%, so we can easily find as 124649.35015039.

Therefore, .

Using and the seconds passed since the last swap () we can calculate the target virtual balances:

1. If the current price is closer to ():

2. In the current price is closer to ():

In the code, we store for convenient, and refer to it as the dailyPriceShiftBase, as it is the base of the exponential function used to update the virtual balances.

If there are no swaps that bring the pool back into range, we need an additional guardrail to prevent the range from shifting “past” the center point. We do this by imposing a minimum value on the “overvalued” token (i.e., the one with the lower balance: o = b in case 1 above, and a in case 2), given by the virtual balance when centeredness = 1:

$V_{o_{min}} = \frac{R_{o}}{\sqrt Q_0-1)}$

# Price Interval Update

Given the new price ratio (), we can calculate the new virtual balances. There are several ways to do this, and we decided to update it keeping the pool centeredness constant. That's because, if pool centeredness is not constant, an update in the price ratio can take the pool from an IN RANGEstate to an OUT OF RANGE state without a user action, so it can introduce inconsistencies when moving the price interval to follow the market price.

To keep the pool centeredness constant, we need to calculate the new virtual balances based on the following (we are using the centeredness if , but a similar derivation applies to the other case):

Since we have , , and , we can calculate and .

1. Isolate in the formula:
2. Isolate in the centeredness formula: (if , centeredness goes in the denominator)
3. Replace formula in the formula, and the result will be:

4. Resolve the formula above with Bhaskara to find the value of , then replace the value of in the formula.

# Calculation of the Virtual Balances

# When initializing the pool

During pool creation, pass minimum and maximum prices of A ( and ), target price . The contract also needs to assume an arbitrary , which we suggest should be 1000 * FixedPoint.ONE.

This allows the pool, during creation, to calculate the virtual balances as:

Note, in the equation above, that . Also, note that and are scaled according to . During the pool initialization, these parameters will be scaled according to the real balances.

Calculate the theoretical balances and for the default .

Calculate the pool centeredness using the parameters above, and check if the pool centeredness is above the margin. If not, reverts.

# Balance Ratio Getter

Between pool creation and initialization, the user must be able to calculate the correct token proportions (i.e., the Balance Ratio) needed to ensure the target price is respected. This balance ratio is given by: .

# Pool initialization

To initialize the pool, we receive the real balances and , and need to validate that , with some margin of error (0.01%).

If this is false, revert. Otherwise, calculate the scale of and , which is . Therefore, and .

Finally, ensure the price is close enough to the target price, and the centeredness is above margin.

# On Swap

When executing onSwap, three steps must be performed:

1. Calculate . If blockTimestamp > endQ0Time, return . Else, calculate based on the formula:

2. Update the virtual balances as follows, keeping the pool centeredness constant. This won't move the pool OUT OF RANGE if there's no swap, which makes off-chain calculations more reliable and optimizes the price interval calculation when the pool is OUT OF RANGE.

   a. Calculate the centerednessFactor () using the method described in the Pool Centeredness section above.

   b. Calculate . It's a Bhaskara formula (notice that there's no minus sign, to avoid issues with unsigned math): - - - -

   c. Calculate . Notice that , so the equation can be simplified to . This simplification is useful, since it allows to be calculated with or .

3. Check whether the pool is OUT OF RANGE

   If so, update the virtual balances using the formulas from the Daily Price Shift Exponent section above. If the virtual balances were updated due to Q0 updating, use the new virtual balances.

IMPORTANT: Notice that Virtual Balances are not recalculated on every swap. This is because rounding issues in the calculation of virtual balances may lead to inconsistencies with the pool invariant and return more tokens to the user, potentially draining the pool.

Since we do not update the virtual balances on swaps, fee collection causes the invariant to grow slowly as the virtual balances remain constant. This slowly increases the price ratio, which has the effect of de-concentrating liquidity. Note that under these conditions, the price ratio will slowly diverge from what was set by the admin. If this is undesirable, the admin can always reset it to the original value, and it will slowly reconcentrate liquidity to the original range.

# On Add/Remove Liquidity

When adding or removing liquidity (which can only be done proportionally), we need to increase the virtual balances in the same proportion that we increased the real balances. That will ensure that the token prices don't change.

In the onBefore[Add|Remove]Liquidity hooks, calculate the proportion as follows:

Use bptOut when adding liquidity, and bptIn when removing it.

Finally, scale virtual balances A and B by this proportion ()

# Calculation of Swap Result

In the equations below, we will replace Token A and Token B by Token In and Token Out .

So, the invariant can be described as

When a swap occurs, the invariant is constant, so

Isolating amountIn and amountOut in the equation above is a prerequisite for calculating the swap result. Notice that all swaps are calculated after the virtual balances are updated (when the price ratio is changing or the pool is out of range).

# Exact In

So, isolating amountOut we have:

We can use the same denominator on the right:

Now, if we expand the multiplications, we have:

All terms except those involving amountIn cancel out, so the final equation is:

# Exact Out

So, isolating amountIn we have:

We can use the same denominator on the right:

Now, if we expand the multiplications, we have:

All terms except those involving amountOut cancel out, so the final equation is: