Readjusting Concentrated Liquidity AMM Pools
Overview
reCLAMM Pools are a type of concentrated liquidity pool that focus liquidity within a predefined price range, allowing LPs to earn greater fees with less capital—especially when the market price remains within that range. This concentration is initialized with a target price and range bounds, enabling the pool to deliver capital efficiency over traditional constant-product models.
What sets reCLAMM apart is its adaptive nature. As trading activity or liquidity operations shift the market price, reCLAMM Pools are able to automatically move their price range—up or down the price curve—without any intervention from users or governance. This "re-centering" behavior activates only when the pool becomes sufficiently unbalanced, based on a margin threshold defined at deployment. Once triggered, the pool begins gradually shifting its range in the direction of market pressure, ensuring liquidity stays useful and active. To enable this adaptive behavior, reCLAMM Pools are configured with a few key parameters:
- A target price, often set near the current market price at deployment.
- A price range, where all the pool’s liquidity is initially concentrated.
- A margin, expressed as a percentage, defining how much imbalance is tolerated before the range begins shifting.
- A daily shift exponent, which controls how quickly the pool adjusts its range when out of balance.
For example, if the margin is set at 20%, the pool tolerates up to a 60/40 imbalance (±10% deviation from a 50/50 balance). Once this threshold is crossed, the pool begins migrating its range incrementally over time, following the market.
This design offers LPs the benefit of concentrated liquidity without the need for manual range resets. It suits passive LPs seeking to stay aligned with market trends while still capturing the fee benefits of a tighter range.
Those familiar with other concentrated liquidity designs may notice echoes of similar mechanisms—like pools that start with fixed ranges around a target price—but unlike those, reCLAMM’s range is not locked. Instead, it evolves in response to the market, maintaining efficiency over time without additional user action.
The following diagram shows a pool that is OUT OF RANGE. The current price is within the price range (as it must be), but above the margin. In this state, the pool will be shifting the price range "up" toward higher prices, following the market, and attempting to bring the market price back inside the margins.
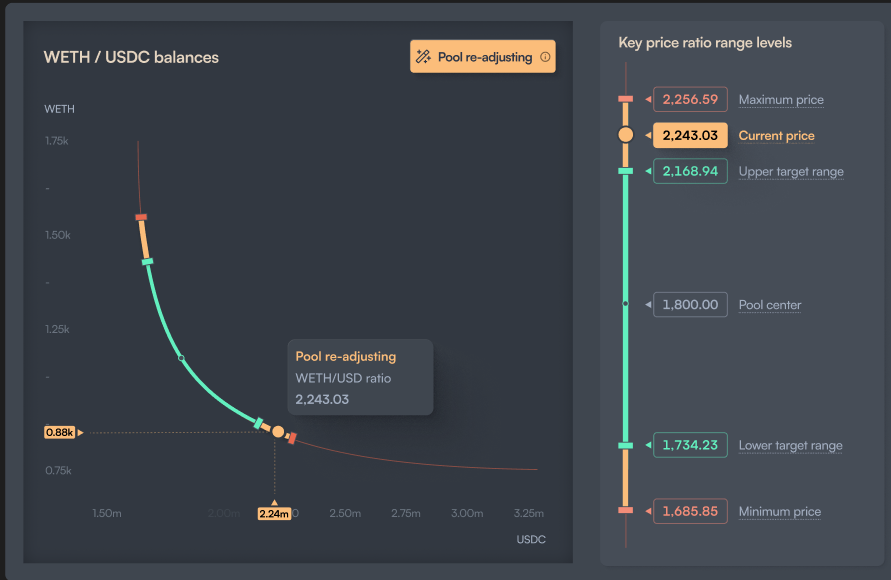
Info
reCLAMM Pools are always two-token pools.
- The minimum swap fee percentage is 0.001% (note - same as the Weighted Pool)
- The maximum swap fee is 10%
- The invariant bounds are unused in this pool, as liquidity can only be added or removed proportionally
- The initialization and other parameters are described in detail below
Note that the swap fee and invariant limits are defined in ReClammPool through implementing the ISwapFeePercentageBounds and IUnbalancedLiquidityInvariantRatioBounds interfaces, which are included in IBasePool.
See here for a more detailed reference.
Advantages of reCLAMM Pools
- All the benefits of concentrated liquidity: higher fees and better capital efficiency (when in range, same math as UniV3)
- None of the maintenance required with traditional concentrated liquidity pools: LP-and-forget
- Moreover, unlike third party ALMs, the rebalancing is entirely transparent
- Fungible positions can be incentivized, making them ideal for guaranteeing deep DAO token liquidity
- Calculations simplified by having all LPs share the same price range
- reCLAMM Pools automatically adjust to market conditions; LPs should always be earning fees
- While designed to be maintenance-free, reCLAMM Pools are tunable by admins if necessary in extreme conditions
These are designed for maintaining deep liquidity, and should not be used for token launches, or with tokens that have low liquidity or otherwise manipulable prices (e.g., using direct collateral or relying on non-aggregated on-chain oracles).
Price range mechanism
One fundamental thing to understand is how the price range is defined and enforced in the first place, given that the price curve is essentially "weighted math" (constant product), and the price is normally determined by the token balances, which are unconstrained (beyond needing to be greater than 0).
The answer is the introduction of "offsets" to the real balances called "virtual" balances, such that the token balances used to calculate the invariant are redefined as the sum of the real and virtual balances. These virtual balances fix the price curve on both ends, cutting off the long tail and ensuring non-zero minimum and maximum prices, even as the real balances approach zero. (This mechanism is shared by Gyro pools, but the terminology here is very slightly different.)
Higher virtual balances (relative to the real balances) means higher concentration.
Initialization
What we really need internally is the "ratio" of the minimum and maximum prices, but since calculating this is unintuitive and a lot to ask of integrators, we created an initialization mechanism that takes very simple input: the actual minimum and maximum prices, and a target price. Two additional parameters are required to specify the behavior of the pool after initialization (margin and price shift exponent); those are described below.
One question that arises immediately is: how do we define the price? There are after all two ways to define the price of a 2-token pool: A in terms of B, or B in terms of A. We have chosen to define the prices as B/A; i.e., prices represent the value of token A denominated in token B. In other words, how many B tokens equal the value of one A token. Since Balancer pool tokens must be registered in numerical order, the "direction" of the ratio is deterministic.
When the pool is created from the factory, these initial values are stored immutably; they are only used during initialization.
The initialization process essentially derives the "internal" parameters from the initial user input, and given the real token balances being supplied, checks that the resulting prices match their intended values: otherwise the pool would be vulnerable to losses through arbitrage.
See the link below for the detailed math, but we start with the definition of the invariant:
And the price, recalling that it is defined as B/A:
We know the desired price ratio (max/min), and we see that these values can be derived by setting each real balance to 0. At the edges, one of the balances will be the maximum value, and the other will be 0. The "maximum balance" is really a placeholder needed for intermediate calculations (it will cancel out later), so we can assign it a convenient arbitrary value (e.g., 1000). Given the invariant and these price bounds, we can derive initial values for the virtual balances.
Recall that the total balances (which determine the actual price) are defined as the sum of the real and virtual balances. We know the virtual balances and the target price, so it is now possible to calculate the "theoretical" real balances that would result in the target price.
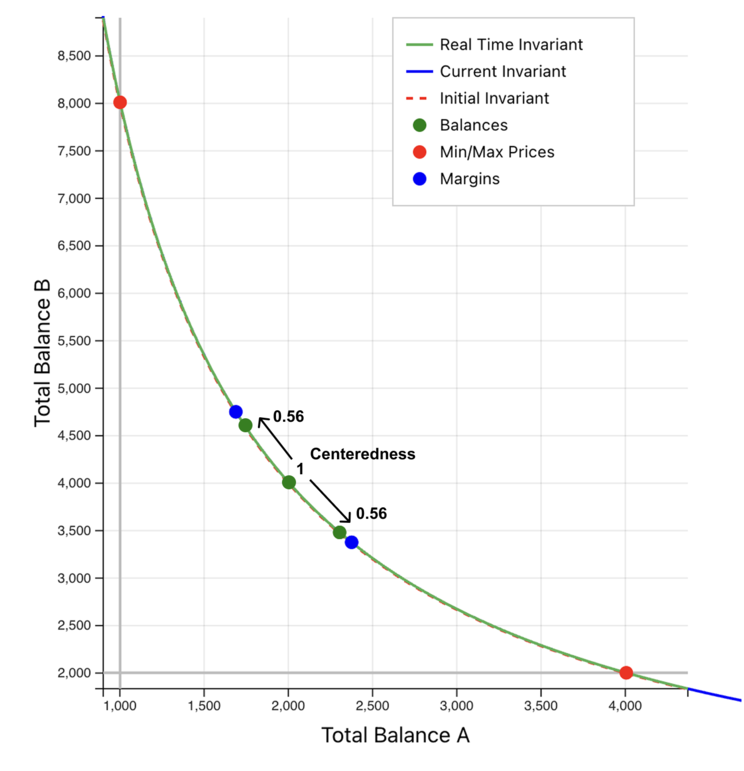
Given this information, we can calculate the "centeredness" of the pool (defined below). This is a measure of balance. A value of 1 means the pool is perfectly balanced, and 0 means it is at one of the edges of the range. We expect that the target price will be roughly in the middle of the target range, so that the initial centeredness is in the neighborhood of 1: but it does not need to be exact. What it does need to be is above the margin: otherwise, the pool would be out of range immediately. If this happens (i.e., the target price is too close to one of the edges), initialization will fail.
The next step is to "scale" the virtual balances. This is basically the inverse of the operation above that calculated the theoretical virtual balances from arbitrary real balances. Now that we know the real token balances the initializer intends to deposit, we can use the ratios determined above to calculate the actual initial virtual balances.
Finally, we validate that the ratio of the real balances corresponds to the theoretical ratio arising from the initial inputs, and that the actual price after initialization closely matches the initial target price. These values might not match exactly, due to rounding or precision errors, so there is a built-in tolerance of 0.01%. If any of these validations fail, initialization reverts, insuring the user against configuration errors.
We provide a helper function, computeInitialBalancesRaw, to assist with these calculations. Given the actual intended deposit amount of one of the tokens - and the initial parameters set on deployment - the contract can calculate how much of the other token must be supplied to pass all the initialization checks.
One final twist involves the handling of wrapped tokens with rate providers, which are expected to be commonly used in reCLAMM Pools. Recall that the prices are passed in during initialization - but how were they calculated? It's possible the pool creator wants to use the direct price of the wrapped token (e.g., for non-boosted pools with tokens like wstETH). In this case, the price does not include the rate provider, even though the token has one. In other cases (e.g., boosted pools with tokens like waUSDC), the creator might want to use the price of the underlying token instead. In that case, the price does incorporate the rate, and the initialization calculation must accommodate that. Accordingly, along with the price range and target values, the pool is deployed with flags indicating whether to use the rate provider for each token during initialization.
Centeredness Margin
The centeredness margin is another parameter that must be set on deployment. Unlike the initial target and range, it is not immutable, and can be changed later by admin action.
This is a percentage value in the range of 0 - 90%. A value of 0 would mean there is effectively no margin - real balances can go to 0, and the pool will never readjust. This degenerate case is effectively the same as a Gyro 2-CLP at the full price range: completely insensitive to price movement, until the pool goes out of range and effectively halts. (Technically, reCLAMM pools act like 2-CLPs constructed with the current range whenever they're in range and not updating the price ratio.)
A value of 100% would mean the pool is always "out of range," unless it is perfectly balanced. This is maximal sensitivity to price changes; essentially it would always be shifting the range (and incurring somewhat higher gas costs). Since the margin can only be changed when the pool is in range both before and after, it would be very difficult to lower it from 100%. Mainly for this reason, the maximum was set to 90%. We expect most pools to be configured somewhere in the middle.
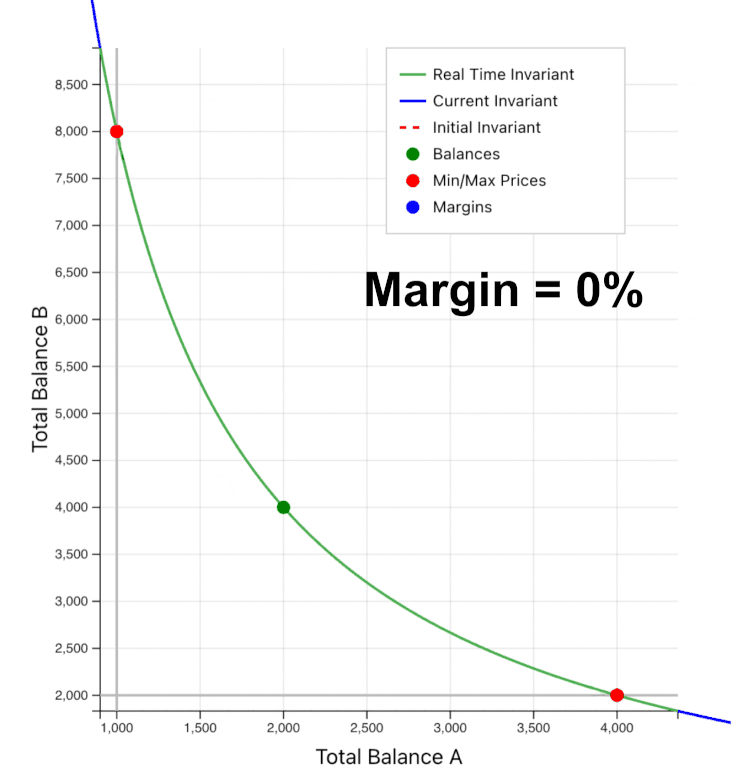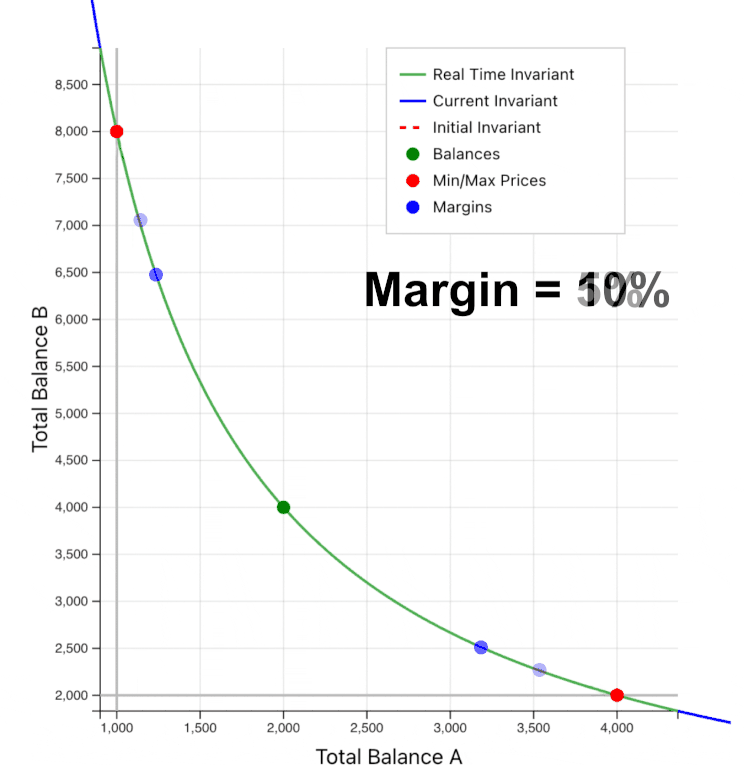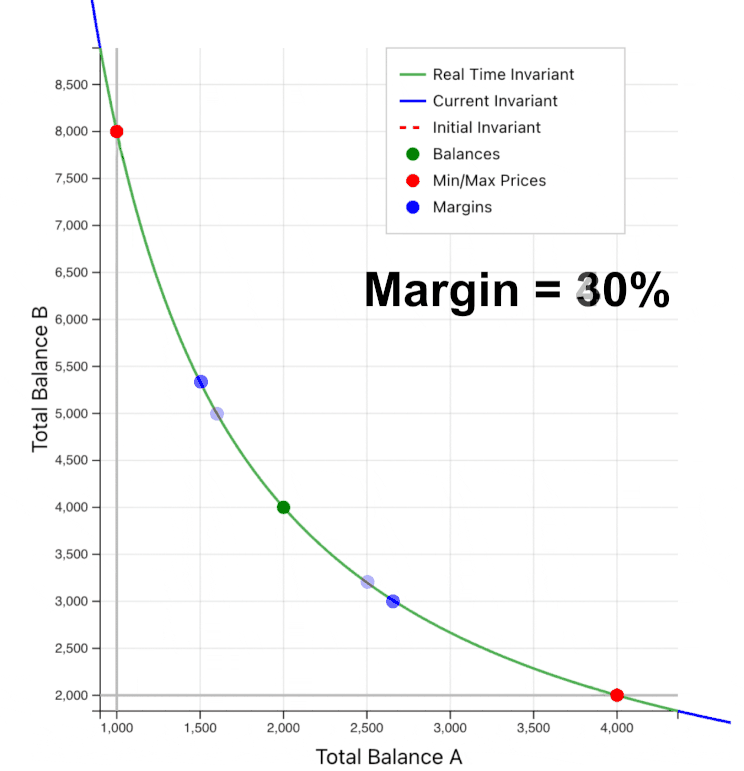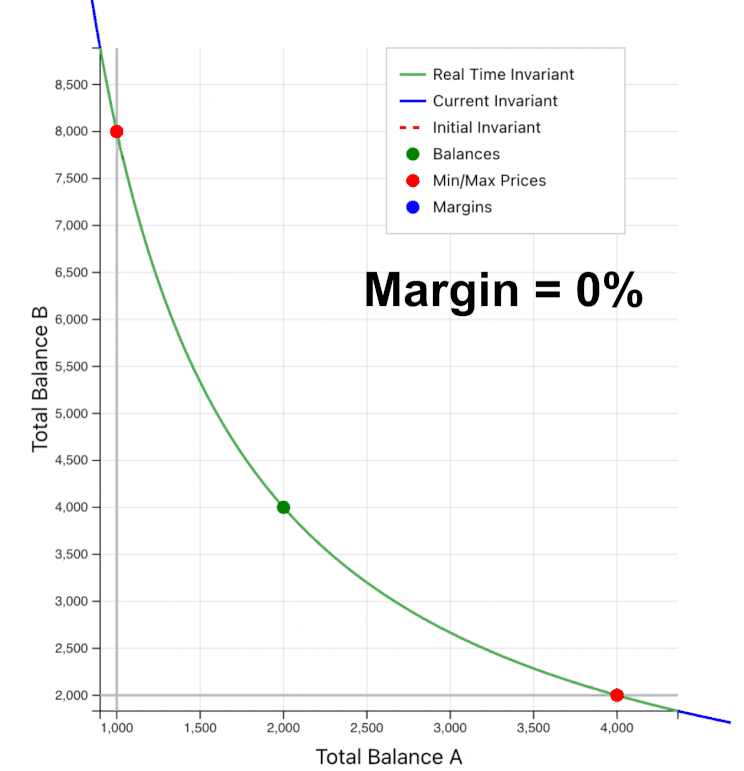
Note that the centeredness measure is symmetric around the center point. On initialization, the pool centeredness should be very close to 1. As swaps move the real balances (with constant virtual balances), the centeredness will move up or down the price curve away from 1 and toward the margins (for these examples, we are using margins from 0 to 50%).
When the centeredness falls below 50%, the market price point will be above the upper or below the lower price margin on the curve, heading toward one of the edges of the price range (where one of the real token balances would be 0).
Daily price shift exponent
The centeredness margin is the final parameter (relating to reCLAMM functionality) that must be set on deployment. Unlike the initial target and range, it is not immutable, and can be changed later by admin action.
This is also a percentage, and it controls the "doubling rate" of the price shift. At 100%, the prices will double (or halve) in one day. This rate is non-linear, and means that the prices will be multiplied (or divided) by 2^(dailyPriceShiftExponent) per day. So 200% corresponds to 2^2 or 4x, and 300% corresponds to 2^3 or 8x. (The maximum is 100%, or doubling once per day.)
Note that the math prevents the price from "overshooting" in either direction due to inactivity (i.e., shifting past the center point, where centeredness equals 1, if there is an extended period with no swaps).
Admin actions
reCLAMM Pool admins can do three things: 1) change the centeredness margin (the threshold for updates); 2) change the daily price shift exponent (the speed of updates); and 3) initiate an update to the price interval (i.e., the distance, or ratio, between the minimum and maximum price bounds), or simply stop an ongoing update. All of these changes will update the virtual balances (and potentially slightly change the price).
All of these functions require the pool to be initialized.
To prevent manipulation, changing the margin also requires the Vault to be locked (i.e., not in the middle of a transaction, which could transiently set balances to arbitrary values), and the pool to be "in range" both before and after. It is not possible to "move the goal posts" by admin action in such a way as to make the pool start or stop an update.
Similarly, the daily price shift exponent can only be changed when the Vault is locked. As it is only altering the speed of the update, it does not check for centeredness. As described above, the price shift exponent is capped at 100% (corresponding to doubling or halving once a day).
Admins can also change the price ratio, supplying the new ratio and a start and end time. There is a minimum duration for the update (1 day), and a minimum amount of ratio change: 1e6 wei. (This is loosely analogous to Uniswap's "tick" resolution limit, introduced for similar reasons.)
These are "best effort" checks to keep the pool well-behaved, but are not hard guarantees. There is also a way to simply stop an ongoing update, which will fix the price ratio at its current value. Note that it is not necessary to stop an ongoing update before starting a new one. Starting an update while one is ongoing is equivalent to stopping and immediately restarting with the new parameters.
Note that it is possible for the price range to be both shifting up or down and expanding or contracting at the same time. Gas costs will be higher during these operations, compared to "in range" swaps with no ongoing price ratio update.
Simulator
A simulator is deployed here. You can set the initial parameters manually - or load them from a real deployed reCLAMM pool, then change the settings to see how a real pool would respond (including simulating swaps).
See this page for details of the math.